Timescale argues that special vector databases are the wrong idea because vectors are more like a special index derived from the data.

“Let the [general] database handle the complexity” of updating that “index” when the data changes. Because it will.

Linda McIver and Cory Doctorow do not buy the AI hype.

McIver ChatGPT is an evolutionary dead end:

As I have noted in the past, these systems are not intelligent. They do not think. They do not understand language. They literally choose a statistically likely next word, using the vast amounts of text they have cheerfully stolen from the internet as their source.

Doctorow’s Autocomplete Worshippers:

AI has all the hallmarks of a classic pump-and-dump, starting with terminology. AI isn’t “artificial” and it’s not “intelligent.” “Machine learning” doesn’t learn. On this week’s Trashfuture podcast, they made an excellent (and profane and hilarious) case that ChatGPT is best understood as a sophisticated form of autocomplete – not our new robot overlord.

Not so fast. First, AI systems do understand text, though not the real-world referents. Although LLMs were trained by choosing the most likely word, they do more. Representations matter. How you choose the most likely word matters. A very large word frequency table could predict the most likely word, but it couldn’t do novel word algebra (king - man + woman = ___) or any of the other things that LLMs do.

Second, McIver and Doctorow trade on their expertise to make their debunking claim: we understand AI. But that won’t do. As David Mandel notes in a recent preprint AI Risk is the only existential risk where the experts in the field rate it riskier than informed outsiders.

Google’s Peter Norvig clearly understands AI. And he and colleagues argue they’re already general, if limited:

Artificial General Intelligence (AGI) means many different things to different people, but the most important parts of it have already been achieved by the current generation of advanced AI large language models such as ChatGPT, Bard, LLaMA and Claude. …today’s frontier models perform competently even on novel tasks they were not trained for, crossing a threshold that previous generations of AI and supervised deep learning systems never managed. Decades from now, they will be recognized as the first true examples of AGI, just as the 1945 ENIAC is now recognized as the first true general-purpose electronic computer.

That doesn’t mean he’s right, only that knowing how LLMs work doesn’t automatically dispel claims.

Meta’s Yann LeCun clearly understands AI. He sides with McIver & Doctorow that AI is dumber than cats, and argues there’s a regulatory-capture game going on. (Meta wants more openness, FYI.)

Demands to police AI stemmed from the “superiority complex” of some of the leading tech companies that argued that only they could be trusted to develop AI safely, LeCun said. “I think that’s incredibly arrogant. And I think the exact opposite,” he said in an interview for the FT’s forthcoming Tech Tonic podcast series.

Regulating leading-edge AI models today would be like regulating the jet airline industry in 1925 when such aeroplanes had not even been invented, he said. “The debate on existential risk is very premature until we have a design for a system that can even rival a cat in terms of learning capabilities, which we don’t have at the moment,” he said.

Could a system be dumber than cats and still general?

McIver again:

There is no viable path from this statistical threshing machine to an intelligent system. You cannot refine statistical plausibility into independent thought. You can only refine it into increased plausibility.

I don’t think McIver was trying to spell out the argument in that short post, but as stated this begs the question. Perhaps you can’t get life from dead matter. Perhaps you can. The argument cannot be, “It can’t be intelligent if I understand the parts”.

Doctorow refers to Ted Chiang’s “instant classic”, ChatGPT Is a Blurry JPEG of the Web

[AI] hallucinations are compression artifacts, but—like the incorrect labels generated by the Xerox photocopier—they are plausible enough that identifying them requires comparing them against the originals, which in this case means either the Web or our own knowledge of the world.

I think that does a good job at correcting many mistaken impressions, and correctly deflating things a bit. But also, that “Blurry JPEG” is key to LLM’s abilities: they are compressing their world, be it images, videos, or text. That is, they are making models of it. As Doctorow notes,

Except in some edge cases, these systems don’t store copies of the images they analyze, nor do they reproduce them.

They gist them. Not necessarily the way humans do, but analogously. Those models let them abstract, reason, and create novelty. Compression doesn’t guarantee intelligence, but it is closely related.

Two main limitations of AI right now:

1. They’re still small. Vast in some ways, but with limited working memory. Andrej Karpathy suggests LLMs are like early 8-bit CPUs. We are still experimenting with the rest of the von Neumann architecture to get a viable system.
2. AI is trapped in a self-referential world of syntax. The reason they hallucinate (image models) or BS (LLMs) is they have no semantic grounding – no external access to ground truth.

Why not use a century of experience with cognitive measures (PDF) to help quantify AI abilities and gaps?

~ ~ ~

Copyright

A interesting tangent: Doctorow’s piece covers copyright. He thinks that

Under these [current market] conditions, giving a creator more copyright is like giving a bullied schoolkid extra lunch money.

…there are loud, insistent calls … that training a machine-learning system is a copyright infringement.

This is a bad theory. First, it’s bad as a matter of copyright law. Fundamentally, machine learning … [is] a math-heavy version of what every creator does: analyze how the works they admire are made, so they can make their own new works.

So any law against this would undo what wins creators have had over conglomerates regarding fair use and derivative works.

Turning every part of the creative process into “IP” hasn’t made creators better off. All that’s it’s accomplished is to make it harder to create without taking terms from a giant corporation, whose terms inevitably include forcing you to trade all your IP away to them. That’s something that Spider Robinson prophesied in his Hugo-winning 1982 story, “Melancholy Elephants”.

Interesting look at speed gains in Python 3.11, by Beshr Kayali. (Who has a microblog! @beshr@m.beshr.com)

Software pushes us to get better as people, on her blog Jessitron.

Background

This was inspired by Paul Harrison’s (pfh’s) 2021 post, We’ve been doing k-means wrong for more than half a century. Pfh found that the K-means algorithm in his R package put too many clusters in dense areas, resulting in worse fits compared with just cutting a Ward clustering at height (k).

tl;dr

I re-implemented much of pfh’s notebook in Python, and found that Scikit-learn did just fine with k-means++ init, but reproduced the problem using naive init (random restarts). Cross-checking with flexclust, he decided the problem was a bug in the LICORS implementation of k-means++.

Upshot: use either Ward clustering or k-means++ to choose initial clusters. In Python you’re fine with Scikit-learn’s default. But curiously the Kward here ran somewhat faster.

Update Nov-2022: I just searched for the LICORS bug. LICORS hasn’t been maintained since 2013, but it’s popular in part for its implementation of kmeanspp , compared to the default (naive) kmeans in R’s stats package. However, it had a serious bug in the distance matrix computation reported by Bernd Fritzke in Nov. 2021 that likely accounts for the behavior Paul noticed. Apparently fixing that drastically improved its performance.

I’ve just created a pull-request to the LICORS package with that fix. It appears the buggy code was copied verbatim into the motifcluster​ package. I’ve added a pull request there.

Summarizing pfh

• k-means tries to minimise sum-of-squared distances of points to clusters
• The usual Lloyd’s algorithm is fast, but gets stuck near the initial guess.
• Initializing by random choice distributes clusters proportional to point density.
• But cluster centers should be more spread out, roughly as density to the power $\frac{d}{d+2}$, where $d$ is number of dimensions.
• k-means++ and Ward both seem to do this.
• In one dimension, fast exact solutions are possible. R:Ckmeans.1d.dp, Python:ckwrap, ckmeans

References

Citation for fastcluster:

Daniel Müllner, fastcluster:Fast Hierarchical, Agglomerative Clustering Routines for R and Python, Journal of Statistical Software 53 (2013), no. 9, 1–18, URL http://www.jstatsoft.org/v53/i09/

Speed depends on many things.

• Note the up-to-1000x improvements in this 2018 discussion of sklearn’s k-means by using Cython, OpenMP, and well-vectorized code. (The ticket is closed with a [MRG] note, so may have been incorporated already.)
• And this 2020 post says Facebook’s faiss library is 8x faster and 27x more accurate than sklearn, at least on larger datasets like MNIST.
• Or a 2017 post for CFXKMeans promising 78x speedup – though note sklearn may have gotten much faster since then.

Test Times & Scores

I’ll omit the code running the tests. Defined null_fit() , do_fits(), do_splice(), functions to run fits and then combine results into a dataframe.

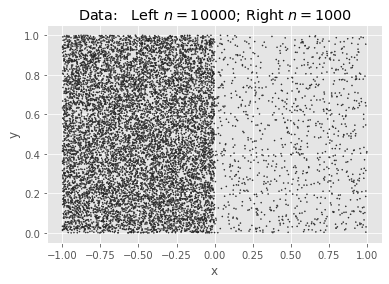
Borrowing an example from pfh, we will generate two squares of uniform density, the first with 10K points and the second with 1K, and find $k=200$ means. Because the points have a ratio of 10:1, we expect the ideal #clusters to be split $\sqrt{10}:1$.

Python

We see the same thing using vanilla k-means (random restarts), but the default k-means++ init overcomes it.

The Data:

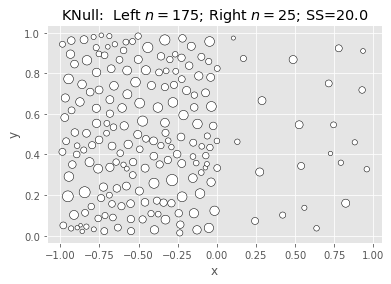
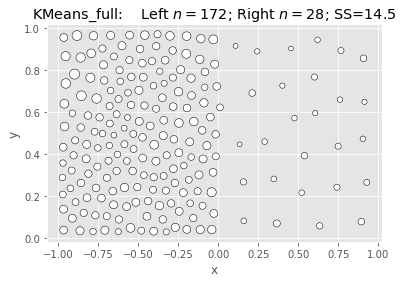
SciKit KMeans: Null & Full (Naive init):

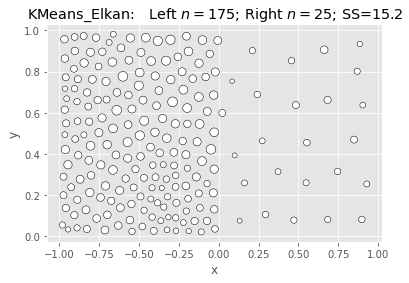
SciKit KMeans: Elkan & Kmeans++:

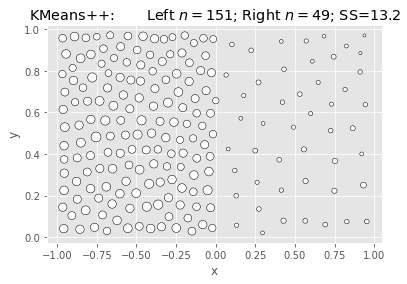
Ward & Polish:

More data: vary $n1, k$

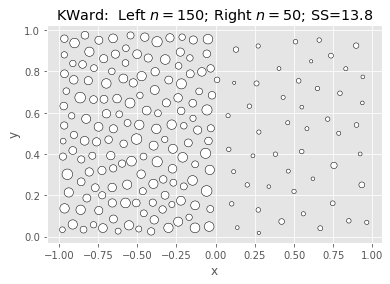
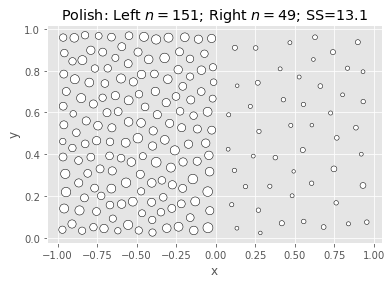
What we’re seeing above is that Ward is fast and nearly as good, but not better.

Let’s collect multiple samples, varying $k$ and $n1$ as we go.

Plot Scores

We will see that KWard+Polish is often competitive on score, but seldom better.

• rows = $k$
• columns = $n1$ (with $n2 = 10 \times n1$

Pfh’s example was for $n1 = 1000$ and $k = 200$.

Plot CPU Times

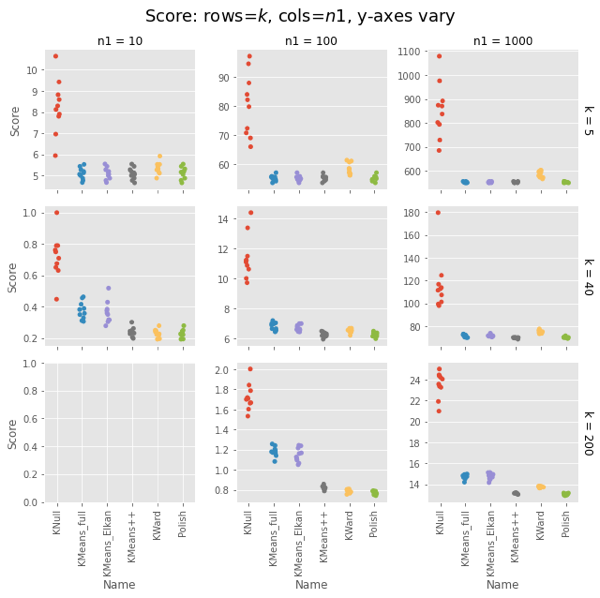
Remember that polish() happens after the Ward clustering, so you should really add those two columns. But in most cases it’s on the order of the KNull.

Even with the polish step, Ward is generally faster, often much faster. The first two has curious exceptions for $n1 = 100, 1000$. I’m tempted to call that setup overhead, except it’s not there for $n1 = 10$, and the charts have different orders of magnitude for the $y$ axis.

Note that the wall-time differences are less extreme, as KMeans() uses concurrent processes. (That helps the polish() step as well, but it usually has few iterations.)

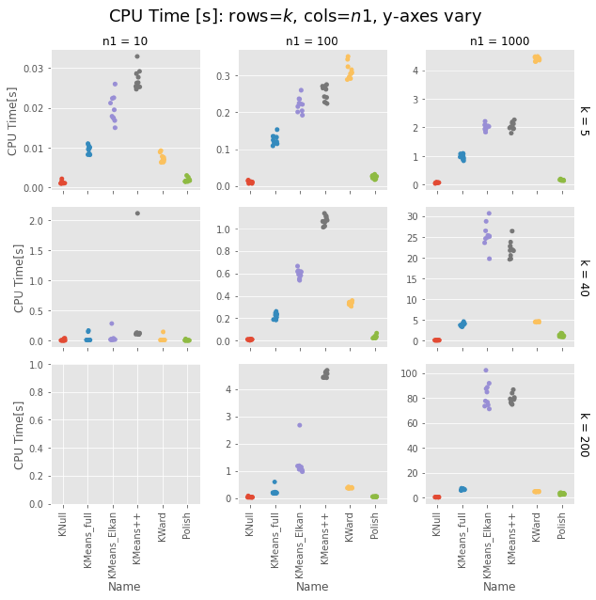
Fair enough: On uniform random data, Ward is as fast as naive K-means and as good as a k-means++ init.

How does it do on data it was designed for? Let’s make some blobs and re-run.

Test with Real Clusters

OK, so that’s how it performs if we’re just quanitizing uniform random noise. What about when the data has real clusters? Saw blob generation on the faiss example post.

Preview of some of the data we’re generating:

Scores

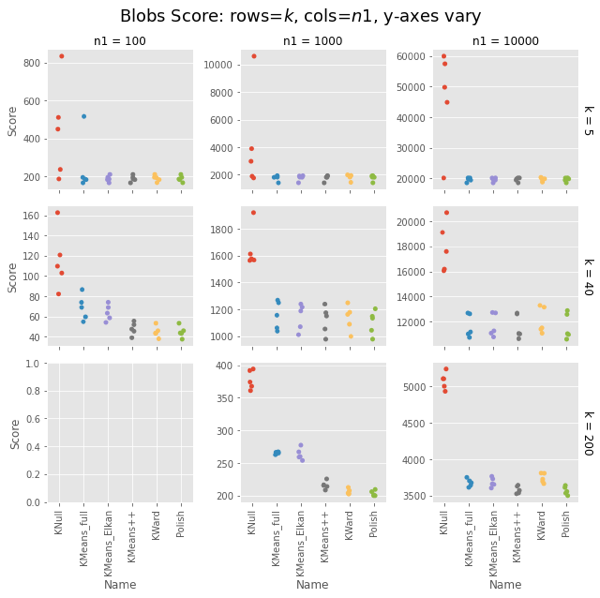
Ward and Polish score on par with KMeans++. For some combinations of $n1$ and $k$ the other algorithms are also on par, but for some they do notably worse.

CPU Times

Ward is constant for a given $n1$, about 4-5s for $n1 = 10,000$. KMeans gets surprisingly slow as $k$ increases, taking 75s vs. Ward’s 4-5s for $k=200$. Even more surprising, Elkan is uniformly slower than full. This could be intepreted vs. compiled, but needs looking into.

The basic result holds.

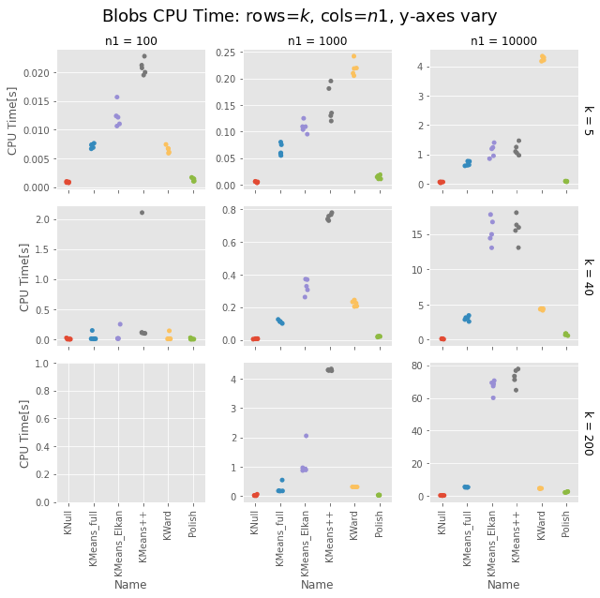
Strangely, Elkan is actually slower than the old EM algorithm, despite having well-organized blobs where the triangle inequality was supposed to help.

Conclusion

On both uniform random data and blob data, KWard+Polish scores like k-means++ while running as fast as vanilla k-means (random restarts).

In uniform data, the polish step seems to be required to match k-means++. In blobs, you can pretty much stop after the initial Ward.

Surprisingly, for sklearn the EM algorithm (algorithm='full') is faster than the default Elkan.

Appendix: the Classes

We defined two classes for the tests:

• KNull - Pick $k$ data points at at random and call that your answer.
• KWard - A drop-in replacement for Scikit-Learn’s KMeans, but uses Ward hierarchical clustering, but at height $k$.

We call the fastcluster package for the actual Ward clustering, and provide a .polish() method to do a few of the usual EM iterations to polish the result.

It gives results comparable to the default k-means++ init, but (oddly) was notably faster for large $k$. This is probably just interpreted versus compiled, but needs some attention. Ward is $O(n^2)$ while k-means++ is $O(kn)$, but Ward was running in 4-5s while scikit-learn’s kmeans ++ was taking notably longer for $k≥10$. For $k=200$ it took 75s. (!!)

The classes are really a means to an end here. The post is probably most interesting as:

• identifying a bug in an R package,
• learning a bit more about what makes K-means solutions good
• finding an odd slowness in scikit-learn’s k-means.

KNull Class

KNull just choses $k$ points at random from $X$. We could write that from scratch, but it’s equivalent to calling KMeans with 1 init and 1 iteration. (Besides, I was making a subclassing mistake in KWard, and this minimal subclass let me track it down.)

class KNull(KMeans):
    """KMeans with only 1 iteration: pick $k$ points from $X$."""
    def __init__(self, 
                 n_clusters: int=3, 
                 random_state: RandLike=None):
        """Initialize w/1 init, 1 iter."""
        super().__init__(n_clusters,
                        init="random",
                        n_init=1,
                        max_iter=1,
                        random_state=random_state)  

Aside: A quick test confirms .inertia_ stores the training .score(mat). Good because it runs about 45x faster.

KWard Class

We make this a subclass of KMeans replacing the fit() method with a call to fastcluster.linkage_vector(X, method='ward') followed by cut_tree(k) to get the initial clusters, and a new polish() method that calls regular KMeans starting from the Ward clusters, and running up to 100 iterations, polishing the fit. (We could put polish() into fit() but this is clearer for testing.

Note: The _vector is a memory-saving variant. The Python fastcluster.linkage*() functions are equivalent to the R fastcluster.hclust*() functions.

class KWard(KMeans):
    """KMeans but use Ward algorithm to find the clusters.
    
    See KMeans for full docs on inherited params.
    
    Parameters
    -----------
    These work as in KMeans:
        n_clusters : int, default=8
        verbose : int, default=0
        random_state : int, RandomState instance, default=None

    THESE ARE IGNORED: 
        init, n_init, max_iter, tol
        copy_x, n_jobs, algorithm
    
    
    Attributes 
    -----------
    algorithm : "KWard"
    
    Else, populated as per KMeans:
        cluster_centers_
        labels_
        inertia_
        n_iter_ ????
    
    Notes
    -------
    Ward hierarchical clustering repeatedly joins the two most similar points. We then cut the
    resulting tree at height $k$.  We use the fast O(n^2) implementation in fastcluster.
        
    """
    def __init__(self, n_clusters: int=8, *,
                 verbose: int=0, random_state=None):
        super().__init__(n_clusters,
                         verbose = verbose, 
                         random_state = random_state)
        self.algorithm = "KWard" # TODO: Breaks _check_params()
        self.polished_ = False
        
    def fit(self, X: np.array, y=None, sample_weight=None):
        """Find K-means cluster centers using Ward clustering.
        
        Set .labels_, .cluster_centers_, .inertia_.
        Set .polished_ = False.
        
        Parameters
        ----------
        X : {array-like, sparse matrix} of shape (n_samples, n_features)
            Passed to fc.linkage_vector.
            
        y : Ignored
        
        sample_weight : Ignored
            TODO: does fc support weights?
        
        """
        # TODO - add/improve the validation/check steps
        X = self._validate_data(X, accept_sparse='csr',
                               dtype=[np.float64, np.float32],
                               order='C', copy=self.copy_x,
                               accept_large_sparse=False)
        
        # Do the clustering. Use pandas for easy add_col, groupby.
        hc = fc.linkage_vector(X, method="ward")
        dfX = pd.DataFrame(X)
        dfX['cluster'] = cut_tree(hc, n_clusters=self.n_clusters)

        # Calculate centers, labels, inertia
        _ = dfX.groupby('cluster').mean().to_numpy()
        self.cluster_centers_ = np.ascontiguousarray(_)
        self.labels_ = dfX['cluster'] 
        self.inertia_ = -self.score(X)
        
        # Return the raw Ward clustering assignment
        self.polished_ = False
        return self
    
    def polish(self, X, max_iter: int=100):
        """Use KMeans to polish the Ward centers. Modifies self!"""
        if self.polished_:
            print("Already polished. Run .fit() to reset.")
            return self
        
        # Do a few iterations
        ans = KMeans(self.n_clusters, n_init=1, max_iter=max_iter,
                     init=self.cluster_centers_)\
                .fit(X)
        
        # How far did we move?
        𝛥c = np.linalg.norm(self.cluster_centers_ - ans.cluster_centers_)    
        𝛥s = self.inertia_ - ans.inertia_
        print(f"   Centers moved by: {𝛥c:8.1f};\n"
              f"  Score improved by: {𝛥s:8.1f} (>0 good).")
        self.labels_ = ans.labels_
        self.inertia_ = ans.inertia_
        self.cluster_centers_ = ans.cluster_centers_
        self.polished_ = True
        return self

Usage: KWard(k).fit(X) or KWard(k).fit(X).polish(X).

Slogan on an ad for scrum training. Featured in the the 2015 talk “Agile is Dead”.

Dave Thomas shows what goes wrong when “Agile” becomes a proper noun, and talks about reclaiming agility.

• Find out where you are.

• Take a small step towards your goal.

• Adjust your understanding based on what you learned.

• Repeat.

• [All things equal], take the path that makes future change easier.

Bookmarking A methodology for agile data science by Edwin Thoen (ch.5 of Agile Data Science with R). Also favors Kanban. Highlights below.

As a rule of thumb, never work on more tasks simultaneously than the number of data scientists on the team.

One of the major pitfalls of trying to improve a data science product is endless exploration of a hypothesis.

How to manage exploration then?

The data scientist should not take longer for the task than the team agreed upfront, wrapping up even when he does not feel completely finished. If he found an alleyway that is still worthwhile exploring a new task should be put in the backlog, instead of persevering in the current task

Bookmarking Why Kanban for data science. Two core issues:

…tasks have uncertain outcomes

…don’t have a good definition of done

Wait… @agilelisa, this is near your domain, no?